Đường Trung Trực Là Gì? Kiến Thức Hình Học Cấp THCS
Đường trung trực là gì
- Khái niệm cơ bản: đường trung trực là gì trong hình học phẳng
- Tính chất quan trọng của đường trung trực là gì:
- Mọi điểm nằm trên đường trung trực đều cách đều hai đầu mút của đoạn thẳng
- Điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực
- Đường trung trực là trục đối xứng của đoạn thẳng
- Ba đường trung trực của tam giác luôn đồng quy tại một điểm
- Vị trí của tâm đường tròn ngoại tiếp phụ thuộc vào loại tam giác
- Đường trung trực là cơ sở của nhiều bài toán quỹ tích
- Ứng dụng của đường trung trực trong thực tế và dựng hình
- Ứng dụng của đường trung trực là gì trong giải toán hình học:
- Mối liên hệ giữa đường trung trực và các yếu tố khác trong tam giác:
Khái niệm cơ bản: đường trung trực là gì trong hình học phẳng
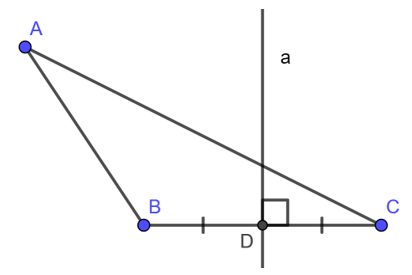
Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của nó. Đây là một trong những khái niệm nền tảng nhất của hình học phẳng, thường được học sinh làm quen ngay từ những lớp đầu cấp hai. Nói cách khác, đường trung trực chính là tập hợp tất cả các điểm trong mặt phẳng cách đều hai đầu mút của đoạn thẳng. Nếu một điểm nằm trên đường trung trực của đoạn thẳng AB thì khoảng cách từ điểm đó đến A và đến B là bằng nhau, tức là MA = MB.
Về mặt hình học, đường trung trực thể hiện tính đối xứng hoàn hảo của đoạn thẳng. Nó chia đoạn thẳng thành hai phần bằng nhau và đồng thời chia mặt phẳng thành hai miền đối xứng qua đường này. Chính nhờ tính chất đó, đường trung trực thường được dùng để xác định các vị trí cân bằng, chia đều khoảng cách, hoặc tìm điểm đối xứng trong nhiều bài toán dựng hình.
>> Xem thêm: Bảng đơn vị đo diện tích
Đường trung trực trong hình học phẳng
Ví dụ cụ thể: Cho đoạn thẳng AB, ta xác định trung điểm M của AB. Khi dựng một đường thẳng vuông góc với AB tại M, ta được đường trung trực của AB. Bất kỳ điểm nào nằm trên đường này, dù ở phía trên hay phía dưới đoạn AB, đều cách đều hai điểm A và B.
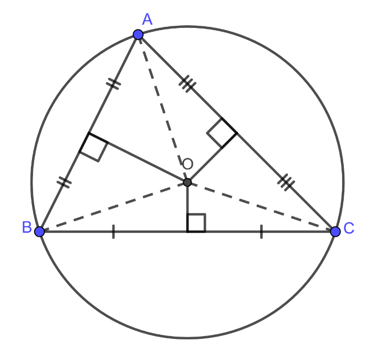
Đường trung trực còn có ứng dụng đặc biệt trong tam giác. Ba đường trung trực của ba cạnh tam giác luôn đồng quy tại một điểm duy nhất, điểm đó được gọi là tâm đường tròn ngoại tiếp tam giác – tức là điểm cách đều ba đỉnh của tam giác. Từ đó, có thể vẽ được đường tròn ngoại tiếp đi qua ba đỉnh ấy. Đây là kiến thức cốt lõi thường xuất hiện trong các bài toán chứng minh hình học, dựng hình hoặc tìm quỹ tích điểm.
Không chỉ trong sách vở, khái niệm đường trung trực còn có nhiều ứng dụng trong thực tế đời sống. Chẳng hạn, khi muốn đặt một cột đèn ở vị trí sao cho nó cách đều hai ngôi nhà, hoặc thiết kế một công viên nằm giữa hai con đường song song, ta đều đang áp dụng nguyên lý của đường trung trực.
Tính chất quan trọng của đường trung trực là gì:
Đường trung trực là một đường đặc biệt trong hình học phẳng, mang nhiều tính chất thể hiện sự cân đối và đối xứng. Những tính chất này không chỉ giúp ta hiểu rõ bản chất của đường trung trực mà còn là nền tảng để giải nhiều dạng bài tập hình học.
Mọi điểm nằm trên đường trung trực đều cách đều hai đầu mút của đoạn thẳng
Nếu điểm M thuộc đường trung trực của đoạn AB thì MA = MB. Đây là tính chất cơ bản nhất, thường được dùng để xác định hoặc chứng minh một điểm nằm trên đường trung trực.
Điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực
Nếu một điểm M bất kỳ trong mặt phẳng thỏa mãn điều kiện MA = MB, thì M nằm trên đường trung trực của đoạn AB. Hai tính chất này tạo thành một cặp thuận – đảo, được dùng thường xuyên trong các bài toán chứng minh hình học.
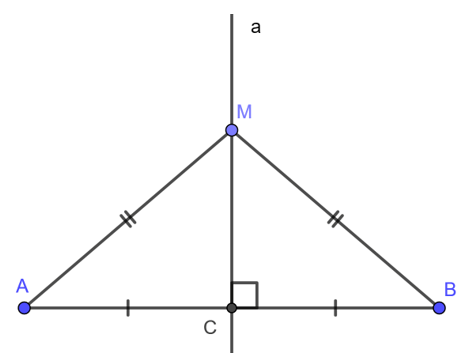
Đường trung trực là trục đối xứng của đoạn thẳng
Đường trung trực chia đoạn thẳng thành hai phần bằng nhau và đồng thời chia mặt phẳng thành hai miền đối xứng. Mọi điểm đối xứng qua đường này đều có khoảng cách bằng nhau đến hai đầu đoạn thẳng, thể hiện rõ đặc trưng cân bằng của nó.
Đường trung trực trong tam giác đặc biệt
Ba đường trung trực của tam giác luôn đồng quy tại một điểm
Ba đường trung trực của ba cạnh trong cùng một tam giác luôn cắt nhau tại một điểm duy nhất, được gọi là tâm đường tròn ngoại tiếp. Điểm này cách đều ba đỉnh của tam giác, nhờ đó ta có thể vẽ được một đường tròn đi qua cả ba đỉnh.
Vị trí của tâm đường tròn ngoại tiếp phụ thuộc vào loại tam giác
Với tam giác nhọn: tâm nằm bên trong tam giác.
Với tam giác vuông: tâm nằm ở trung điểm của cạnh huyền.
Với tam giác tù: tâm nằm bên ngoài tam giác.
Đường trung trực là cơ sở của nhiều bài toán quỹ tích
Tập hợp các điểm trong mặt phẳng cách đều hai điểm cố định A và B chính là đường trung trực của AB. Nhờ tính chất này, ta có thể xác định nhanh quỹ tích điểm trong nhiều bài toán hình học, đặc biệt ở chương trình lớp 7.
Ứng dụng của đường trung trực trong thực tế và dựng hình
Nguyên lý của đường trung trực được dùng khi cần chia đôi khoảng cách, tìm vị trí cân bằng, hay dựng hình có tính đối xứng. Trong kỹ thuật và kiến trúc, nó giúp đảm bảo sự chính xác khi thiết kế các công trình hoặc bộ phận cơ khí.
Ứng dụng của đường trung trực là gì trong giải toán hình học:
Đường trung trực là một trong những công cụ hình học quan trọng và được sử dụng rất nhiều trong các bài toán từ cơ bản đến nâng cao. Việc hiểu rõ cách ứng dụng của đường trung trực giúp học sinh rèn luyện tư duy chứng minh, kỹ năng dựng hình, cũng như khả năng quan sát quan hệ giữa các yếu tố hình học.
1. Ứng dụng trong bài toán chứng minh hình học
Đường trung trực thường được dùng để chứng minh hai đoạn thẳng bằng nhau. Nếu hai điểm cùng nằm trên đường trung trực của một đoạn thẳng, ta có thể dễ dàng suy ra chúng cách đều hai đầu mút của đoạn đó. Ví dụ, trong tam giác, khi cần chứng minh hai đỉnh cách đều một cạnh nào đó, ta có thể dựa vào tính chất của đường trung trực.
2. Ứng dụng trong dựng hình bằng thước và compa
Khi cần chia đôi một đoạn thẳng hoặc xác định điểm cân bằng giữa hai vị trí, đường trung trực là công cụ trực tiếp nhất. Việc dựng đường trung trực của đoạn AB giúp tìm trung điểm M của đoạn thẳng, từ đó có thể dựng các hình có tính đối xứng như hình vuông, tam giác cân hoặc tam giác đều.
3. Ứng dụng trong xác định tâm đường tròn ngoại tiếp
Ba đường trung trực của tam giác luôn đồng quy tại một điểm, đó là tâm đường tròn ngoại tiếp. Ứng dụng này rất quan trọng trong các bài toán về đường tròn, giúp xác định vị trí tâm hoặc bán kính của đường tròn đi qua ba đỉnh tam giác. Trong bài toán thực tế, nguyên lý này còn được dùng để xác định vị trí chính giữa của ba điểm cho trước.
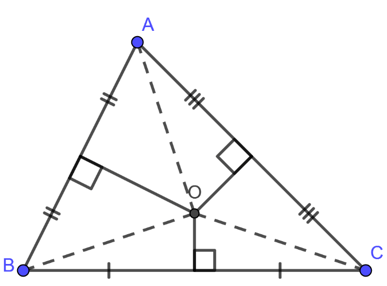
Tâm đường tròn ngoại tiếp đồng thời là trực tâm
4. Ứng dụng trong bài toán quỹ tích điểm
Một trong những ứng dụng nổi bật của đường trung trực là trong dạng bài tìm quỹ tích. Khi đề bài yêu cầu xác định tất cả các điểm cách đều hai điểm A và B, quỹ tích đó chính là đường trung trực của đoạn AB. Đây là một trong những bài toán cơ bản nhưng mang tính nền tảng để phát triển các bài quỹ tích phức tạp hơn.
5. Ứng dụng trong nhận biết các loại tam giác
Dựa vào vị trí giao nhau của các đường trung trực, ta có thể nhận biết loại tam giác: nếu tâm đường tròn ngoại tiếp nằm trong tam giác thì tam giác nhọn, nếu nằm trên cạnh huyền thì tam giác vuông, còn nếu nằm ngoài thì tam giác tù. Điều này giúp học sinh hiểu sâu hơn về mối liên hệ giữa các yếu tố hình học.
Mối liên hệ giữa đường trung trực và các yếu tố khác trong tam giác:
Trong hình học phẳng, tam giác là hình có nhiều yếu tố đặc biệt như đường trung tuyến, đường cao, đường phân giác, và đường trung trực. Mỗi loại đường có tính chất riêng, nhưng chúng luôn tồn tại mối liên hệ chặt chẽ với nhau. Việc hiểu rõ mối quan hệ giữa đường trung trực và các yếu tố khác giúp người học nắm vững cấu trúc của tam giác và vận dụng hiệu quả trong bài toán chứng minh hay dựng hình.
1. Mối liên hệ giữa đường trung trực và đường trung tuyến
Cả hai đều đi qua trung điểm của một cạnh trong tam giác.
Tuy nhiên, đường trung tuyến nối trung điểm cạnh đó với đỉnh đối diện, còn đường trung trực lại vuông góc với cạnh tại trung điểm.
Trong tam giác cân, đường trung trực và đường trung tuyến của cạnh đáy trùng nhau, vì đỉnh đối diện nằm trên đường vuông góc chia đôi đáy.
2. Mối liên hệ giữa đường trung trực và đường cao
Đường cao là đường vuông góc hạ từ một đỉnh xuống cạnh đối diện.
Trong tam giác vuông, đường cao từ đỉnh góc vuông cũng đồng thời là đường trung trực của cạnh huyền, bởi nó vừa vuông góc vừa đi qua trung điểm của cạnh huyền.
Điều này cho thấy sự kết hợp đặc biệt giữa hai loại đường trong một dạng tam giác cụ thể.
3. Mối liên hệ giữa đường trung trực và đường phân giác
Đường phân giác chia một góc của tam giác thành hai góc bằng nhau, trong khi đường trung trực chia một cạnh thành hai phần bằng nhau và vuông góc với cạnh đó.
Trong tam giác đều, do các góc và các cạnh đều bằng nhau, nên ba đường phân giác, ba đường trung trực, ba đường cao và ba trung tuyến đều trùng nhau.
Điều này thể hiện tính đối xứng hoàn hảo của tam giác đều và là lý do vì sao loại tam giác này thường được dùng để minh họa các tính chất hình học cơ bản.
4. Mối liên hệ giữa đường trung trực và tâm đường tròn ngoại tiếp
Ba đường trung trực của ba cạnh tam giác luôn đồng quy tại một điểm gọi là tâm đường tròn ngoại tiếp.
Tâm này là điểm duy nhất trong tam giác cách đều cả ba đỉnh.
Nhờ mối quan hệ này, ta có thể dễ dàng dựng được đường tròn ngoại tiếp nếu biết ba đỉnh của tam giác, hoặc ngược lại, xác định vị trí của một đỉnh khi biết tâm và hai đỉnh còn lại.
>> Tham khảo: Giá làm răng giả nguyên hàm


