Đường trung trực là một trong những kiến thức nền tảng quan trọng của hình học, thường xuất hiện trong chương trình Toán THCS và THPT. Mặc dù khái niệm đơn giản, nhưng đường trung trực lại được ứng dụng rất nhiều trong chứng minh hình học, dựng hình, tìm tâm đường tròn ngoại tiếp và nhiều bài toán thực tế liên quan đến khoảng cách. Bài viết dưới đây sẽ giúp bạn hiểu chi tiết đường trung trực là gì, tính chất, cách vẽ, ví dụ bài tập và những lỗi mà học sinh thường gặp. 

Khái Niệm Đường Trung Trực Là Gì?

Trong hình học phẳng, đường trung trực của đoạn thẳng AB được định nghĩa như sau:

Đường trung trực của AB là đường thẳng vuông góc với AB tại trung điểm của đoạn thẳng đó.

Để hình dung dễ hơn, ta có thể tách khái niệm này thành hai phần:

Trung: đi qua trung điểm M của đoạn thẳng AB.

Trực: vuông góc với đoạn thẳng AB tại chính trung điểm M.

Tức là nếu M là trung điểm của AB, thì đường trung trực là đường thẳng qua M đồng thời vuông góc với AB.

Công thức trung điểm của AB trong hệ tọa độ:

Nếu A(x1, y1) và B(x2, y2), thì trung điểm M có tọa độ

M((x1 + x2) / 2 , (y1 + y2) / 2)

Khái niệm đường trung trực là gì thường được sử dụng khi:

Cần so sánh khoảng cách từ một điểm đến hai điểm khác

Cần chứng minh hai đoạn thẳng bằng nhau

Cần dựng đường tròn ngoại tiếp tam giác

Cần xác định vị trí điểm cách đều hai mút đoạn thẳng

Nhờ tính chất cách đều này mà đường trung trực là chủ đề quan trọng trong nhiều bài hình học.

>> Tham khảo:  Tổng cấp số nhân

Định nghĩa đường trung trực là gì?

Tính Chất Quan Trọng Của Đường Trung Trực

Đường trung trực sở hữu hai tính chất cơ bản nhưng vô cùng mạnh mẽ. Đây cũng là hai tính chất xuất hiện trong hầu hết các bài chứng minh.

Tính chất 1: Mọi điểm nằm trên đường trung trực đều cách đều hai điểm A và B

Nói cách khác, nếu điểm P thuộc đường trung trực của AB, thì:

PA = PB

Nghĩa là khoảng cách từ P đến A bằng khoảng cách từ P đến B.

Tính chất 2: Mọi điểm cách đều A và B đều nằm trên đường trung trực

Nghĩa là nếu có điểm P sao cho PA = PB, thì P luôn nằm trên đường trung trực của AB.

Hai tính chất này tạo thành định lý thuận – đảo. Nhờ đó, ta có thể chứng minh và xác định vị trí một điểm mà không cần tính đo phức tạp.

Ví dụ:

Giả sử ta có tam giác ABC và biết CA = CB. Từ tính chất trên, ta suy ra C nằm trên đường trung trực của AB. Nhờ đó, đường trung trực là một công cụ mạnh để chứng minh tam giác cân hoặc xác định tâm đối xứng.

Đường trung trực trong tam giác

Cách Vẽ Đường Trung Trực Chính Xác Và Nhanh

Có hai cách vẽ phổ biến: dùng thước – compa hoặc dùng hệ tọa độ.

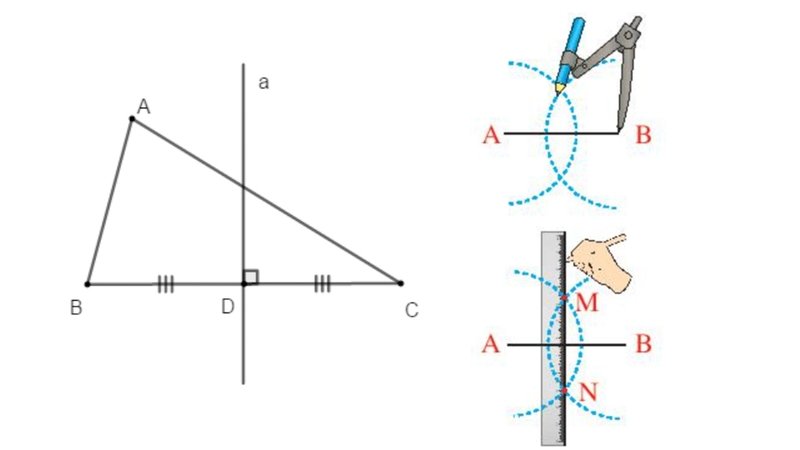
Cách 1: Vẽ bằng thước và compa

Bước 1: Xác định đoạn thẳng AB.

Bước 2: Dùng compa đặt tâm tại A, vẽ một cung tròn lớn có bán kính lớn hơn AB/2.

Bước 3: Giữ nguyên bán kính đó, đặt tâm tại B và vẽ thêm một cung tròn cắt hai cung đầu tiên tại hai điểm C và D.

Bước 4: Nối C và D. Đường thẳng CD chính là đường trung trực của AB.

Cách 2: Vẽ bằng tọa độ

Bước 1: Tính trung điểm M((x1 + x2) / 2 , (y1 + y2) / 2).

Bước 2: Tính vector chỉ phương của AB: u = (x2 – x1, y2 – y1).

Bước 3: Chọn một vector vuông góc với AB, chẳng hạn v = (y1 – y2, x2 – x1).

Bước 4: Đường trung trực là đường đi qua M và có hướng theo vector v.

Ví Dụ Bài Tập Về Đường Trung Trực là gì?

Ví dụ :

Cho đoạn thẳng AB, điểm P thỏa mãn PA = PB. Hãy chứng minh P nằm trên đường trung trực của AB.

Giải

PA = PB ⇒ P cách đều hai điểm A và B.

Theo tính chất đảo của đường trung trực, P nằm trên đường trung trực.

Ví dụ 2:

Trong tam giác ABC, đường trung trực của AB cắt cạnh BC tại D. Chứng minh DA = DB.

Giải:

Vì D thuộc đường trung trực của AB nên DA = DB theo tính chất 1.

Ví dụ 3 (ứng dụng thực tế):

Bạn muốn đặt một trạm phát wifi sao cho nó cách đều hai phòng A và B.

Vị trí tối ưu sẽ nằm trên đường trung trực của đoạn nối hai phòng.

Ứng dụng này mô tả cách sử dụng tính chất khoảng cách trong đời sống thực.

Đường trung trực trong hình học phẳng

Ứng Dụng Đường Trung Trực Trong Hình Học Nâng Cao

Đường trung trực không chỉ xuất hiện trong hình học cơ bản mà còn đóng vai trò quan trọng ở các bài toán nâng cao.

Ứng dụng 1: Tìm tâm đường tròn ngoại tiếp tam giác

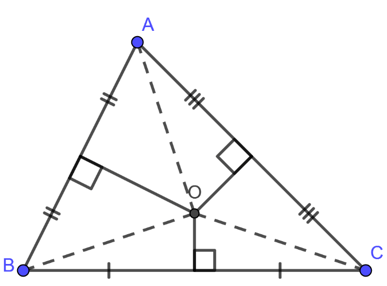
Trong tam giác ABC, ba đường trung trực của các cạnh AB, BC và CA cắt nhau tại một điểm duy nhất.

Điểm đó được gọi là tâm đường tròn ngoại tiếp tam giác.

Do tâm đường tròn ngoại tiếp cách đều A, B, C nên nó nằm trên đường trung trực của tất cả các cạnh.

Ứng dụng 2: Dựng hình

Khi muốn dựng điểm cách đều hai điểm A và B, chỉ cần dựng đường trung trực của AB.

Cách này thường dùng trong các bài dựng hình bằng thước và compa.

Ứng dụng 3: Mô hình hóa khoảng cách trong bản đồ

Trong các thuật toán định vị, đường trung trực xuất hiện như ranh giới giữa hai vùng điểm gần A hơn hoặc gần B hơn.

Đây cũng là cơ sở để tạo bản đồ Voronoi – một dạng phân chia không gian theo khoảng cách.

Ứng dụng 4: Xác định hình chiếu vuông góc

Trong nhiều bài toán đường cao và trung tuyến, đường trung trực hỗ trợ chứng minh tính vuông góc và đối xứng của các điểm.

Sai Lầm Thường Gặp Khi Học Về Đường Trung Trực

Nhầm lẫn giữa đường trung trực và đường phân giác

Nhiều học sinh nghĩ rằng đường trung trực cũng là đường phân giác.

Thực tế:

Đường trung trực: chia đôi đoạn thẳng và vuông góc với đoạn thẳng.

Đường phân giác: chia đôi góc.

Hai khái niệm hoàn toàn khác nhau và dùng cho mục đích khác nhau.

Nhầm trung điểm

Khi vẽ đường trung trực, chỉ cần trung điểm sai là đường vẽ sẽ sai.

Nguyên nhân thường do:

Đo AB không chính xác

Kẻ đường vuông góc tại sai vị trí

Không dùng compa đúng cách

Hiểu sai tính chất cách đều

Một số học sinh nhầm rằng điểm cách đều hai đoạn hoặc hai góc cũng nằm trên đường trung trực.

Thực tế chỉ đúng khi hai khoảng cách là khoảng cách đến hai điểm A và B.

Lẫn lộn với đường cao và trung tuyến

Đôi khi trong tam giác cân, đường cao, trung tuyến và đường trung trực trùng nhau.

Điều này khiến học sinh nhầm lẫn, nghĩ rằng tam giác nào cũng vậy.

Đường Trung Trực Trong Tam Giác – Kiến Thức Bổ Sung Quan Trọng

Trong tam giác, đường trung trực của ba cạnh luôn đồng quy tại một điểm.

Điểm đồng quy này chính là tâm đường tròn ngoại tiếp.

Tọa độ tâm O nếu biết tọa độ A, B, C có thể được xác định bằng hệ phương trình cách đều:

OA = OB

OB = OC

Khi giải hệ hai phương trình trên, ta sẽ tìm được tọa độ của O.

Mặc dù đây là kiến thức nâng cao, nhiều giáo viên vẫn dùng để rèn luyện tư duy hình học tọa độ, đặc biệt trong chương trình lớp 10 và 11.

Ý Nghĩa Thực Tế Của Đường Trung Trực Trong Đời Sống

Mặc dù là một đối tượng hình học thuần túy, đường trung trực lại mang nhiều ứng dụng trong thực tế.

Định vị và tối ưu khoảng cách

Khi cần chọn vị trí đặt nhà kho, trạm thu phí, trạm phát wifi… sao cho khoảng cách đến hai vị trí khác nhau được tối ưu, người ta sử dụng đường trung trực.

Thiết kế và đo đạc công trình

Trong kỹ thuật xây dựng, đường trung trực được dùng để xác định vị trí cân đối, vuông góc và đối xứng của các hạng mục.

Công nghệ bản đồ số

Trong việc phân vùng dữ liệu theo khoảng cách, các thuật toán dựa trên đường trung trực để xác định ranh giới giữa hai khu vực ảnh hưởng của điểm A và điểm B.

Đường trung trực là khái niệm cơ bản nhưng cực kỳ quan trọng trong hình học. Hiểu rõ đường trung trực là gì, tính chất, cách vẽ và ứng dụng sẽ giúp học sinh tự tin hơn trong các bài toán chứng minh, bài dựng hình và bài nâng cao về tam giác. Không chỉ có giá trị trong môn học, đường trung trực còn xuất hiện trong nhiều mô hình thực tế liên quan đến tối ưu khoảng cách và thiết kế công trình.