Tổng Cấp Số Nhân Là Gì? Giải Thích Chi Tiết Và Ví Dụ Minh Họa

Cấp số nhân là gì?
Trong chương trình Toán học THPT, cấp số nhân là một trong những kiến thức nền tảng của Đại số lớp 11. Đây là dạng dãy số xuất hiện thường xuyên trong các bài kiểm tra, bài thi học kỳ và đặc biệt là trong các đề thi tốt nghiệp THPT.
Cấp số nhân được hiểu là một dãy số trong đó mỗi số hạng kể từ số hạng thứ hai đều được tạo thành bằng cách nhân số hạng đứng trước với một số không đổi, gọi là công bội.
Định nghĩa cấp số nhân
Một dãy số được gọi là cấp số nhân nếu tồn tại một số không đổi q sao cho với mọi số hạng từ số hạng thứ hai trở đi, ta có số hạng sau bằng số hạng trước nhân với q.
Số q được gọi là công bội của cấp số nhân. Số hạng đầu tiên thường được ký hiệu là u₁.
Công thức số hạng tổng quát của cấp số nhân
Số hạng thứ n của cấp số nhân được xác định theo công thức:
uₙ = u₁ × qⁿ⁻¹
Công thức này giúp xác định nhanh bất kỳ số hạng nào của cấp số nhân khi biết số hạng đầu và công bội. Đây là nền tảng quan trọng để học sinh tiếp cận các bài toán về tổng cấp số nhân.
Tổng cấp số nhân là gì?
Sau khi hiểu rõ khái niệm cấp số nhân, nội dung tiếp theo và quan trọng hơn chính là tổng cấp số nhân. Đây là phần kiến thức được sử dụng rất nhiều trong bài tập và các bài toán thực tế.
Tổng cấp số nhân là tổng của một số hữu hạn hoặc vô hạn các số hạng liên tiếp trong một cấp số nhân. Việc tính tổng giúp giải quyết các bài toán liên quan đến cộng dồn, tăng trưởng, lãi suất và nhiều hiện tượng trong thực tế.
Ý nghĩa
Tổng cấp số nhân giúp đơn giản hóa việc tính toán khi phải cộng nhiều số hạng có quy luật nhân liên tiếp. Thay vì tính từng số hạng rồi cộng lại, người học chỉ cần áp dụng công thức là có thể tìm được kết quả nhanh chóng và chính xác.
Trong chương trình học, thường xuất hiện trong các bài toán yêu cầu tính tổng n số hạng đầu hoặc xác định một đại lượng chưa biết thông qua tổng.
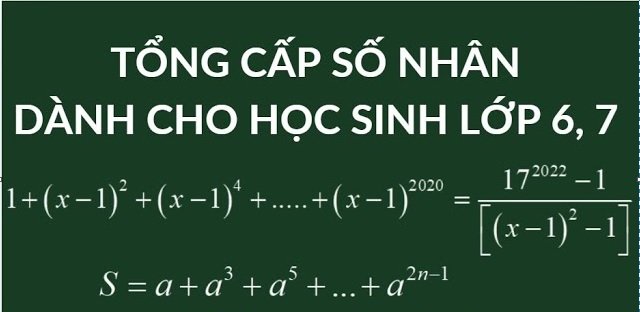
Kiến thức cho học sinh lớp 6 7
Công thức tính tổng cấp số nhân
Để giải các bài toán liên quan, học sinh cần nắm vững công thức tính tổng. Đây là công cụ quan trọng giúp xử lý nhanh các bài toán từ cơ bản đến nâng cao.
Công thức tổng n số hạng đầu của cấp số nhân
Giả sử một cấp số nhân có số hạng đầu là u₁ và công bội là q, tổng của n số hạng đầu được ký hiệu là Sₙ và được tính theo công thức:
Sₙ = u₁ × (1 − qⁿ) / (1 − q) với q ≠ 1
Công thức này cho phép tính nhanh tổng của nhiều số hạng mà không cần liệt kê từng số.
Trường hợp đặc biệt khi công bội bằng 1
Khi công bội q bằng 1, cấp số nhân trở thành một dãy gồm các số bằng nhau. Khi đó, tổng n số hạng đầu được tính theo công thức:
Sₙ = n × u₁
Việc nhận diện đúng trường hợp này giúp tránh áp dụng sai công thức và gây nhầm lẫn khi làm bài.
Cách chứng minh và suy ra công thức
Không chỉ học thuộc công thức, việc hiểu cách chứng minh và suy ra công thức giúp học sinh nắm vững bản chất và ghi nhớ lâu hơn.
Ý tưởng chứng minh công thức
Giả sử Sₙ là tổng của n số hạng đầu của một cấp số nhân:
Sₙ = u₁ + u₁q + u₁q² + … + u₁qⁿ⁻¹
Nhân cả hai vế của biểu thức trên với q, ta thu được một biểu thức mới. Sau đó, lấy biểu thức ban đầu trừ đi biểu thức vừa nhân q, ta sẽ loại bỏ được các số hạng trung gian.
Suy ra công thức tổng
Sau khi thực hiện phép trừ hai biểu thức, ta thu được một phương trình đơn giản chỉ còn hai số hạng đầu và cuối. Từ đó, dễ dàng suy ra công thức tổng n số hạng đầu của cấp số nhân.
Cách chứng minh này thường xuất hiện trong sách giáo khoa và giúp học sinh hiểu rõ nguồn gốc của công thức thay vì chỉ học thuộc máy móc.

Công thức
Các dạng bài tập thường gặp về cấp số nhân
Bài tập về rất đa dạng và có thể phân loại thành nhiều dạng khác nhau. Việc nhận diện đúng dạng bài giúp học sinh lựa chọn phương pháp giải phù hợp.
Dạng tính tổng khi biết số hạng đầu và công bội
Đây là dạng bài cơ bản nhất. Đề bài cho số hạng đầu và công bội, yêu cầu tính tổng n số hạng đầu. Với dạng này, học sinh chỉ cần áp dụng đúng công thức và tính toán cẩn thận.
Dạng tìm số hạng đầu hoặc công bội
Một số bài toán không cho trực tiếp số hạng đầu hoặc công bội mà cung cấp tổng và một vài điều kiện khác. Khi đó, học sinh cần thiết lập phương trình từ công thức tổng để tìm ẩn số.
Dạng bài kết hợp với số hạng tổng quát
Dạng này yêu cầu kết hợp công thức số hạng tổng quát và công thức tổng. Học sinh cần tư duy logic và nắm vững cả hai công thức để giải chính xác.
Dạng bài toán thực tế
Đây là dạng bài nâng cao, thường gắn với các tình huống như lãi suất, tăng trưởng dân số, phân rã phóng xạ. Việc nhận ra mô hình cấp số nhân là chìa khóa để giải bài.

Học sinh trong giờ
Ứng dụng của cấp số nhân trong thực tế
Không chỉ xuất hiện trong sách giáo khoa, còn có nhiều ứng dụng quan trọng trong đời sống và các lĩnh vực khoa học.
Ứng dụng trong tài chính và lãi suất
Trong các bài toán lãi suất kép, số tiền sau mỗi kỳ tăng lên theo một tỷ lệ cố định. Tổng số tiền tích lũy sau nhiều kỳ chính là một bài toán
Ứng dụng trong tăng trưởng và suy giảm
Các hiện tượng tăng trưởng dân số, lan truyền thông tin hoặc suy giảm phóng xạ đều có thể được mô tả bằng cấp số nhân. Cấp số nhân giúp ước tính tổng số lượng sau một khoảng thời gian nhất định.
Ứng dụng trong khoa học và kỹ thuật
Trong vật lý, hóa học và tin học, nhiều quá trình lặp có quy luật nhân liên tiếp. Việc sử dụng giúp đơn giản hóa việc tính toán và dự đoán kết quả.
Cấp số nhân là một nội dung quan trọng trong chương trình Toán học THPT, vừa mang tính lý thuyết vừa có nhiều ứng dụng thực tiễn. Việc hiểu rõ cấp số nhân là gì, nắm vững công thức tính tổng và các dạng bài tập thường gặp sẽ giúp học sinh học tốt phần kiến thức này.
Thay vì học thuộc công thức một cách máy móc, người học nên tập trung hiểu bản chất, cách suy ra công thức và luyện tập thường xuyên để vận dụng linh hoạt trong các bài toán từ cơ bản đến nâng cao.
>> Tham khảo: Bảng giá các loại răng giả


