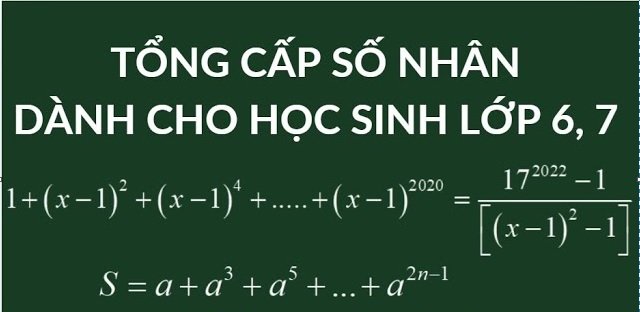
Trong chương trình Đại số THCS và THPT, cấp số nhân là dạng dãy số quen thuộc, xuất hiện trong nhiều bài tập tính toán lũy thừa, lãi kép, mô hình tăng trưởng và cả các bài toán nâng cao. Trong đó, dạng bài phổ biến nhất là tính tổng cấp số nhân. Nếu học sinh không nắm chắc công thức hoặc cách nhận dạng sẽ rất dễ nhầm lẫn với tổng cấp số cộng.

Tổng Cấp Số Nhân Là Gì?

Để hiểu , trước hết ta nhắc lại khái niệm cấp số nhân.

Một dãy số được gọi là cấp số nhân nếu mỗi số hạng (từ số hạng thứ hai) bằng số hạng đứng trước nhân với một số không đổi. Số không đổi này được gọi là công bội, ký hiệu là r.

Nếu a là số hạng đầu tiên, thì cấp số nhân có dạng:

a, ar, ar², ar³, …, arⁿ⁻¹

Khi đó,  Sₙ là tổng của n số hạng đầu tiên:

Sₙ = a + ar + ar² + ar³ + … + arⁿ⁻¹

Đây là dạng tổng thường gặp nhất và cũng là dạng mà giáo viên, học sinh và cả các bài toán thực tế thường sử dụng.

>> Xem thêm:  Quy đồng mẫu số lớp 4

Khái niệm 

Công Thức Tổng Quát

Công thức  có hai trường hợp: r khác 1 và r bằng 1.

Các công thức dưới đây dùng ký tự thuần, có thể copy vào WordPad không lỗi.

Trường hợp 1: Khi r ≠ 1

Sₙ = a(1 – rⁿ) / (1 – r)

Trường hợp 2: Khi r = 1

Khi r = 1 thì mọi số hạng đều bằng a, vì vậy tổng chỉ là:

Sₙ = n × a

Đây là hai công thức kinh điển mà bất kỳ học sinh nào cũng cần ghi nhớ khi giải bài toán tổng cấp số nhân.

Giải Thích Công Thức 

Công thức Sₙ = a(1 – rⁿ) / (1 – r) được suy ra từ việc nhân và trừ hai phương trình:

Sₙ = a + ar + ar² + … + arⁿ⁻¹

rSₙ = ar + ar² + ar³ + … + arⁿ

Lấy Sₙ – rSₙ, ta được:

Sₙ(1 – r) = a(1 – rⁿ)

Suy ra:

Sₙ = a(1 – rⁿ) / (1 – r)

Giải thích đơn giản này giúp học sinh ghi nhớ lâu hơn và hiểu bản chất của công thức, tránh tình trạng học vẹt.

ỨNg dụng vào đời sống

Cách Tính Từng Bước

Bước 1: Xác định số hạng đầu a

Đây là giá trị bắt đầu của dãy.

Bước 2: Xác định công bội r

Công bội r = (số hạng sau) / (số hạng trước).

Nếu chỉ cho hai số hạng cách nhau, ta có thể dùng tỉ lệ.

Bước 3: Xác định n – số lượng số hạng

Đề bài có thể cho trực tiếp hoặc cho số hạng cuối để suy ra.

Bước 4: Áp dụng đúng công thức tương ứng

r = 1 dùng công thức riêng

r ≠ 1 dùng công thức tổng quát

Bước 5: Tính toán cẩn thận rⁿ

Nhiều học sinh nhầm lẫn ở bước này, đặc biệt khi r là phân số hoặc số âm.

Định nghĩa công thức

Ví Dụ Bài Tập Có Lời Giải Chi Tiết

Dưới đây là các ví dụ chi tiết giúp bạn hiểu cách áp dụng công thức vào từng loại bài.

Ví dụ 1

Cho cấp số nhân có a = 3, r = 2. Tính S₅.

Giải:

Ta có n = 5.

S₅ = a(1 – r⁵) / (1 – r)

S₅ = 3(1 – 2⁵) / (1 – 2)

S₅ = 3(1 – 32) / (-1)

S₅ = 3(-31) / (-1) = 93

Kết quả: S₅ = 93

Ví dụ 2:

Cho cấp số nhân có các số hạng: 5, 10, 20, 40, … Tính S₄.

Giải

a = 5

r = 10 / 5 = 2

n = 4

S₄ = 5(1 – 2⁴) / (1 – 2)

S₄ = 5(1 – 16) / (-1)

S₄ = 5(-15) / (-1) = 75

Kết quả: S₄ = 75

Ví dụ 3:

Cho cấp số nhân: 8, 4, 2, 1,… Tính tổng 4 số đầu.

Giải:

a = 8

r = 4 / 8 = 1/2

n = 4

S₄ = 8(1 – (1/2)⁴) / (1 – 1/2)

S₄ = 8(1 – 1/16) / (1/2)

S₄ = 8[(15/16)] × 2

S₄ = 8 × (15/8) × 2 = 30

Kết quả: S₄ = 30

Ví dụ 4 (ứng dụng lãi kép):

Bạn gửi 1.000.000 đồng vào tài khoản, cứ mỗi tháng tăng 5% so với tháng trước. Hỏi tổng số tiền tăng thêm trong 12 tháng là bao nhiêu?

Tăng thêm mỗi tháng tạo thành cấp số nhân với:

a = khoản tăng tháng đầu = 1.000.000 × 0.05 = 50.000

r = 1.05

n = 12

Tổng tăng thêm trong 12 tháng:

S₁₂ = 50.000(1 – 1.05¹²) / (1 – 1.05)

Lưu ý: Mẫu âm nên kết quả dương.

Học sinh có thể lấy máy tính để ra giá trị chính xác.

Đây là ứng dụng thực tế rất phổ biến của tổng cấp số trong tài chính.

Ứng Dụng Của Tổng Cấp Số Nhân Trong Thực Tế

Ứng dụng trong lãi kép

Đây là ứng dụng phổ biến nhất. Mỗi kỳ tăng theo tỉ lệ r tạo thành cấp số nhân, và tổng lãi nhiều kỳ 

Ứng dụng trong tăng trưởng dân số

Mô hình tăng đều theo phần trăm của năm trước cũng tạo ra cấp số nhân.

Ứng dụng trong công nghệ và tin học

Các thuật toán nhân đôi, tăng số bước lặp theo mức gấp rút đều dựa trên cấp số nhân.

Ứng dụng trong khoa học tự nhiên

Phản ứng hóa học nhân đôi, khuếch đại, phân rã phóng xạ… đều mô tả bằng dạng cấp số nhân.

Ứng dụng trong đời sống

Tiền lương tăng theo % mỗi năm, lượng người tham gia sự kiện tăng theo quảng cáo, mức lan truyền của thông tin – đều có thể mô tả bằng cấp số nhân.

Tổng Vô Hạn Của Cấp Số Nhân

Ngoài tổng hữu hạn Sₙ, ta còn có tổng vô hạn (vô cùng nhiều số hạng).

Tổng cấp số vô hạn chỉ tồn tại khi |r| < 1.

Khi đó, công thức tổng là:

S = a / (1 – r)

Ví dụ:

1/2 + 1/4 + 1/8 + 1/16 + …

a = 1/2, r = 1/2

S = (1/2) / (1 – 1/2) = (1/2) / (1/2) = 1

Ý nghĩa: dãy có vô hạn số hạng nhưng tổng của nó vẫn là số hữu hạn.

Những Lỗi Thường Gặp Khi Tính

Nhầm lẫn giữa cấp số nhân và cấp số cộng

Nhiều học sinh dùng nhầm công thức:

Tổng cấp số cộng: Sₙ = n(a + aₙ) / 2

Tổng cấp số nhân: Sₙ = a(1 – rⁿ) / (1 – r)

Nhầm giá trị công bội r

Ví dụ 3, 6, 12 thì r = 2 chứ không phải 3.

Sai khi tính rⁿ

Đây là lỗi phổ biến nhất, đặc biệt khi r là phân số hoặc số âm.

Dùng sai công thức khi r = 1

Nhiều bạn vẫn dùng a(1 – rⁿ)/(1 – r), dẫn đến mẫu bằng 0.

Không xác định chính xác số hạng thứ n

Ví dụ dãy từ 2 đến 32 với công bội 2 nhưng không tính đúng n = 5.

 

Bỏ qua dấu âm khi r < 0

Ví dụ r = -2 thì rⁿ phụ thuộc vào n chẵn hay lẻ.

Bảng Tóm Tắt Công Thức

Tổng n số hạng đầu cấp số nhân:

Sₙ = a + ar + ar² + … + arⁿ⁻¹

Nếu r ≠ 1: Sₙ = a(1 – rⁿ) / (1 – r)

Nếu r = 1: Sₙ = n × a

Tổng vô hạn khi |r| < 1:

S = a / (1 – r)

Những công thức này đều dùng ký tự thuần, dễ copy sang WordPad, Google Docs hoặc trình soạn thảo khác.

Tổng cấp số nhân là dạng kiến thức quan trọng và có nhiều ứng dụng trong toán học cũng như đời sống thực tế. Chỉ cần hiểu rõ khái niệm, nắm chắc công thức và luyện tập một số ví dụ, học sinh sẽ dễ dàng giải được hầu hết các dạng bài liên quan đến cấp số nhân, từ cơ bản đến nâng cao.