Tổng cấp số nhân là gì? Công thức, ví dụ minh họa và bài tập chi tiết.

Trong toán học, đặc biệt là chương trình lớp 11, tổng cấp số nhân là một kiến thức quan trọng giúp ta tính nhanh tổng của dãy số có quy luật nhân liên tiếp. Hiểu và vận dụng công thức cấp số nhân giúp giải quyết hiệu quả nhiều bài toán thực tế. Cùng tham khảo chi tiết qua bài viết dưới đây.
Tổng cấp số nhân
Tổng cấp số nhân là gì?
Cấp số nhân là tổng của các số hạng liên tiếp trong một cấp số nhân, tức là dãy số mà tỷ số giữa hai số hạng liên tiếp luôn không đổi.
Nếu ta có một cấp số nhân gồm các số hạng:
u₁, u₂, u₃, …, uₙ
với công bội là q (tức là u₂ = u₁·q, u₃ = u₂·q = u₁·q², …), thì cấp số nhân gồm n số hạng đầu tiên được viết là:
Sₙ = u₁ + u₂ + u₃ + … + uₙ
Tổng này thể hiện tổng cộng giá trị của n số hạng đầu tiên trong dãy, giúp ta tính nhanh kết quả mà không cần cộng thủ công từng số.
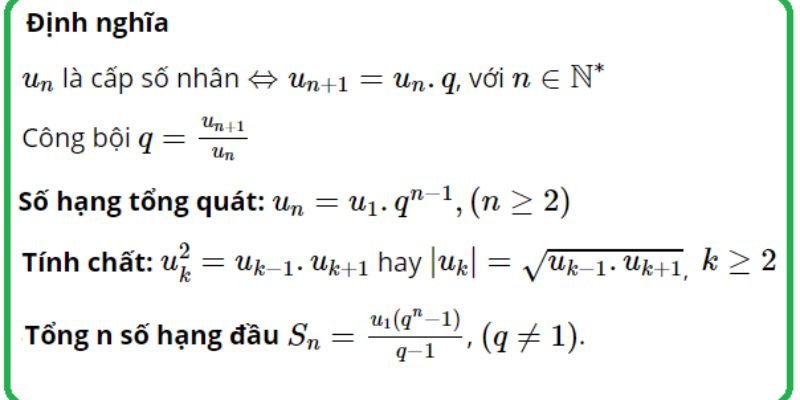
Công thức cấp số nhân
Công thức tính cấp số nhân được xác định như thế nào?
Giả sử ta có một cấp số nhân gồm n số hạng đầu tiên:
u₁, u₂, u₃, …, uₙ
với công bội là q (q ≠ 0). Khi đó, tổng của n số hạng đầu tiên được ký hiệu là Sₙ.
- Trường hợp công bội q ≠ 1
Công thức tổng quát:
Sₙ = u₁ × (qⁿ − 1) ÷ (q − 1)
hoặc viết tương đương là:
Sₙ = u₁ × (1 − qⁿ) ÷ (1 − q)
Hai công thức trên hoàn toàn tương đương, chỉ khác cách trình bày — bạn có thể chọn tùy theo yêu cầu bài toán.
- Trường hợp công bội q = 1
Khi q = 1, các số hạng trong dãy đều bằng nhau (u₁ = u₂ = … = uₙ), khi đó tổng được tính đơn giản bằng:
Sₙ = n × u₁
- Trường hợp cấp số nhân vô hạn (|q| < 1)
Nếu cấp số nhân có vô số số hạng và |q| < 1, tức là giá trị các số hạng càng nhỏ dần, tổng của cấp số nhân này sẽ hội tụ đến một giá trị hữu hạn, được tính bởi công thức:
S = u₁ ÷ (1 − q)
Các công thức trên giúp ta tính nhanh tổng của cấp số nhân hữu hạn hoặc vô hạn mà không cần cộng từng số hạng. Đây là kiến thức quan trọng trong chương Cấp số nhân của Toán học lớp 11, đồng thời có nhiều ứng dụng trong tài chính, vật lý và tin học.

Cách chứng minh công thức cấp số nhân
>> Xem thêm: Đường trung trực là gì
Cách chứng minh công thức cấp số nhân ra sao?
Giả sử ta có một cấp số nhân gồm n số hạng đầu tiên:
u₁, u₂, u₃, …, uₙ
với công bội là q (q ≠ 1). Khi đó, tổng của n số hạng đầu tiên được ký hiệu là:
Sₙ = u₁ + u₂ + u₃ + … + uₙ
Sₙ = u₁ + u₁·q + u₁·q² + … + u₁·qⁿ⁻¹
Bước 1: Nhân cả hai vế của phương trình trên với q:
q·Sₙ = u₁·q + u₁·q² + u₁·q³ + … + u₁·qⁿ
Bước 2: Lấy phương trình thứ hai trừ cho phương trình thứ nhất:
(q·Sₙ) − Sₙ = (u₁·q + u₁·q² + … + u₁·qⁿ) − (u₁ + u₁·q + u₁·q² + … + u₁·qⁿ⁻¹)
Sau khi rút gọn, tất cả các số hạng ở giữa triệt tiêu, ta còn lại:
(q − 1)·Sₙ = u₁·(qⁿ − 1)
Bước 3: Chia hai vế cho (q − 1), ta được công thức tổng cấp số nhân hữu hạn:
Sₙ = u₁ × (qⁿ − 1) ÷ (q − 1)
Bước 4: Trường hợp đặc biệt khi q = 1
Nếu q = 1, nghĩa là các số hạng đều bằng nhau (u₁ = u₂ = … = uₙ), khi đó tổng được tính đơn giản:
Sₙ = n × u₁
Công thức cấp số nhân được chứng minh dựa trên phép nhân và trừ hai vế, giúp rút gọn dãy số một cách ngắn gọn và chính xác. Đây là phương pháp suy luận cơ bản trong toán học, thường được áp dụng khi tìm công thức tổng quát của các dãy có quy luật nhân liên tiếp.
Các dạng bài tập về cấp số nhân
Các dạng bài tập về cấp số nhân
Trong chương trình Toán học lớp 11, phần cấp số nhân thường xuất hiện với nhiều dạng bài khác nhau, từ cơ bản đến nâng cao. Dưới đây là các dạng bài tiêu biểu giúp bạn nắm vững kiến thức và luyện tập hiệu quả.
Dạng 1: Tính tổng của n số hạng đầu tiên của cấp số nhân
Cách làm:
Xác định các yếu tố: số hạng đầu tiên u₁, công bội q, và số lượng số hạng n.
Áp dụng công thức:
Sₙ = u₁ × (qⁿ − 1) ÷ (q − 1) (khi q ≠ 1)
hoặc Sₙ = n × u₁ (khi q = 1)
Ví dụ:
Cho cấp số nhân có u₁ = 3, q = 2, n = 5.
Khi đó: S₅ = 3 × (2⁵ − 1) ÷ (2 − 1) = 3 × 31 = 93.
Dạng 2: Tìm số hạng đầu tiên, công bội hoặc số lượng số hạng khi biết tổng
Cách làm:
Sử dụng công thức tổng Sₙ = u₁ × (qⁿ − 1) ÷ (q − 1).
Thay các dữ kiện đã biết, sau đó giải phương trình để tìm ẩn cần thiết (u₁, q hoặc n).
Ví dụ:
Một cấp số nhân có tổng S₄ = 30, công bội q = 2. Hãy tìm u₁.
Ta có: 30 = u₁ × (2⁴ − 1) ÷ (2 − 1)
⟹ u₁ = 30 ÷ 15 = 2.
Dạng 3: Tính tổng vô hạn của cấp số nhân (|q| < 1)
Cách làm:
Khi cấp số nhân có vô số số hạng và |q| < 1, áp dụng công thức:
S = u₁ ÷ (1 − q)
Ví dụ:
Cho cấp số nhân có u₁ = 8, q = 0.5.
Tổng vô hạn: S = 8 ÷ (1 − 0.5) = 8 ÷ 0.5 = 16.
Dạng 4: Bài toán thực tế liên quan đến tổng cấp số nhân
Cách làm:
Chuyển bài toán thực tế về dạng cấp số nhân (ví dụ: tiền lãi kép, quãng đường vật chuyển động, độ sáng, âm thanh…).
Xác định u₁, q, n hoặc |q| < 1 rồi áp dụng công thức phù hợp.
Ví dụ:
Một người gửi 5 triệu đồng vào ngân hàng, lãi suất 10%/năm, lãi nhập gốc mỗi năm.
Sau 4 năm, tổng số tiền là:
S₄ = 5 × (1.1⁴ − 1) ÷ (1.1 − 1) = 5 × (1.4641 − 1) ÷ 0.1 = 23.2 (triệu đồng).
Dạng 5: So sánh hai cấp số nhân hoặc hai tổng khác nhau
Cách làm:
Tính từng tổng riêng biệt bằng công thức tổng.
Sau đó so sánh giá trị Sₙ của hai dãy theo yêu cầu đề bài (lớn hơn, nhỏ hơn hoặc bằng nhau).
Các dạng bài tập về cấp số nhân rất phong phú, từ việc tính toán cơ bản đến vận dụng thực tế. Việc nắm vững công thức và hiểu rõ bản chất cấp số nhân sẽ giúp bạn giải nhanh, chính xác và đạt điểm cao trong các bài kiểm tra, thi học kỳ hoặc thi tốt nghiệp.
Ứng dụng của cấp số nhân trong thực tế là gì?
Tổng cấp số nhân không chỉ là kiến thức toán học trừu tượng, mà còn có rất nhiều ứng dụng thực tiễn trong đời sống, kinh tế, kỹ thuật và khoa học. Việc hiểu rõ bản chất của cấp số nhân giúp ta mô hình hóa, dự đoán và tính toán chính xác nhiều hiện tượng trong tự nhiên và xã hội.
- Ứng dụng trong tính lãi kép ngân hàng
Trong tài chính, lãi kép là một ví dụ điển hình của cấp số nhân.
Giả sử bạn gửi số tiền ban đầu là u₁, với lãi suất mỗi kỳ là r (tức là công bội q = 1 + r).
Tổng số tiền sau n kỳ được tính bằng:
Sₙ = u₁ × (qⁿ − 1) ÷ (q − 1)
Nhờ công thức này, ta có thể tính tổng tiền gốc và lãi sau nhiều kỳ mà không cần cộng dồn thủ công.
Ví dụ: Gửi 10 triệu đồng, lãi suất 10%/năm, sau 5 năm:
S₅ = 10 × (1.1⁵ − 1) ÷ (1.1 − 1) = 10 × 6.1051 = 61.051 (triệu đồng lãi cộng dồn).
- Ứng dụng trong vật lý – chuyển động tăng tốc đều theo cấp số nhân
Một số hiện tượng vật lý, như chuyển động của vật trong môi trường có lực cản hoặc tăng tốc theo tỷ lệ phần trăm, tuân theo quy luật cấp số nhân.
Ví dụ: vận tốc hoặc quãng đường mỗi giây tăng lên gấp đôi, gấp ba lần so với giây trước — khi đó tổng quãng đường vật đi được chính là cấp số nhân.
- Ứng dụng trong tin học và công nghệ
Trong lĩnh vực máy tính và truyền thông, tốc độ xử lý hoặc dung lượng bộ nhớ có thể tăng theo cấp số nhân theo định luật Moore.
Tổng cấp số nhân giúp ước lượng tổng khả năng xử lý hoặc dung lượng sau nhiều chu kỳ tăng trưởng liên tục.
Ví dụ: nếu dung lượng chip tăng gấp đôi mỗi 2 năm, ta có thể tính tổng dung lượng tích lũy sau nhiều giai đoạn bằng công thức cấp số nhân.
- Ứng dụng trong sinh học và dân số học
Tốc độ sinh sản của vi sinh vật, hoặc sự tăng trưởng dân số theo tỷ lệ phần trăm hàng năm, cũng là một ví dụ về cấp số nhân.
Tổng số cá thể sau n thế hệ hoặc tổng dân số tích lũy qua nhiều năm có thể được tính bằng công thức cấp số nhân.
- Ứng dụng trong âm thanh, ánh sáng và kỹ thuật số
Trong các hệ thống âm thanh hoặc kỹ thuật số, cường độ âm, độ sáng, hoặc mức tín hiệu thường thay đổi theo tỷ lệ nhân (dB, logarit). Khi đó, tổng năng lượng hoặc tổng cường độ cũng có thể biểu diễn dưới dạng cấp số nhân, giúp tối ưu hóa thiết bị điện tử và hệ thống chiếu sáng.
Qua bài viết trên, chúng ta đã hiểu rõ cấp số nhân là gì, nắm vững công thức tính cũng như các ứng dụng thực tế của nó trong đời sống và học tập. Việc thành thạo cách vận dụng công thức cấp số nhân sẽ giúp bạn giải nhanh các bài toán lãi kép, tăng trưởng hay bài tập đại số, đồng thời củng cố nền tảng vững chắc cho các phần kiến thức nâng cao hơn.
>> Tham khảo: Điều trị tủy răng Hà Nội


