Đường trung trực là gì? Cách vẽ, tính chất và ví dụ minh họa chi tiết.

Trong quá trình học hình học, chắc hẳn bạn đã nhiều lần bắt gặp khái niệm đường trung trực, một yếu tố quen thuộc nhưng vô cùng quan trọng. Vậy đường trung trực là gì và nó có những tính chất, cách vẽ như thế nào? Cùng tham khảo bài viết dưới đây để biết thông tin chi tiết nhé!
Đường trung trực là gì
Đường trung trực là gì?
Đường trung trực của một đoạn thẳng là đường thẳng đi qua trung điểm của đoạn thẳng đó và vuông góc với đoạn thẳng ấy. Nói cách khác, đường trung trực chia đoạn thẳng thành hai phần bằng nhau và tạo với đoạn thẳng một góc vuông (90°) tại trung điểm.
Mỗi điểm nằm trên đường trung trực đều có khoảng cách bằng nhau đến hai đầu mút của đoạn thẳng, đây chính là tính chất cơ bản giúp nhận biết và ứng dụng đường trung trực trong các bài toán hình học.
Trong hình học phẳng, đường trung trực thường được sử dụng để xác định tâm đường tròn ngoại tiếp tam giác, giải bài toán dựng hình, hoặc chứng minh hai đoạn thẳng bằng nhau. Đặc biệt, trong một tam giác, ba đường trung trực của ba cạnh luôn cắt nhau tại một điểm duy nhất, điểm đó gọi là tâm đường tròn ngoại tiếp tam giác.
>> Tham khảo: Tổng cấp số nhân
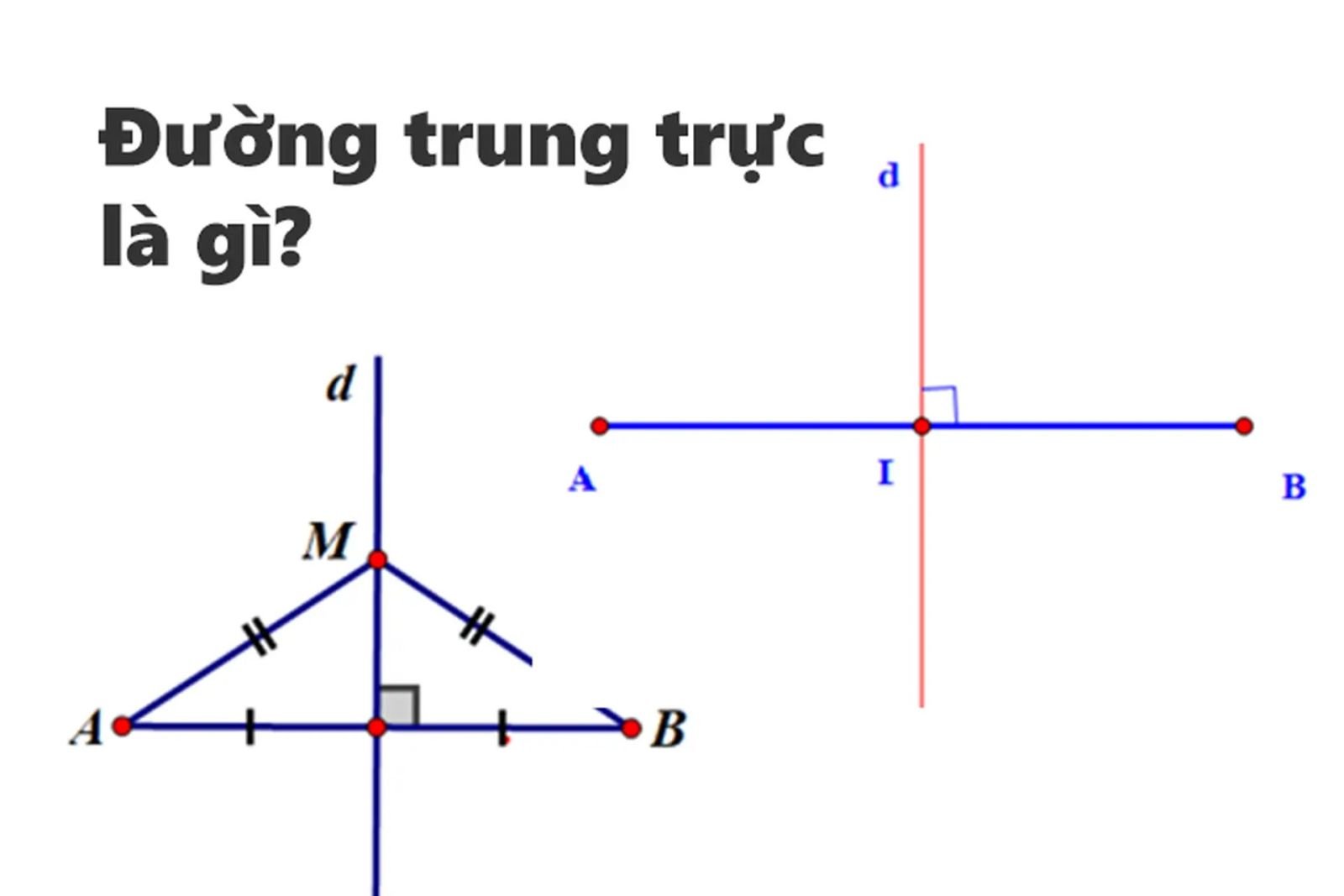
Đường trung trực của một đoạn thẳng
Cách vẽ đường trung trực của đoạn thẳng như thế nào?
Đường trung trực của một đoạn thẳng là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với nó. Đây là một khái niệm cơ bản trong hình học, thường được học ở cấp THCS, và có nhiều ứng dụng trong các bài toán dựng hình, chứng minh hình học cũng như trong đời sống thực tế.
Để vẽ chính xác đường trung trực của một đoạn thẳng, bạn có thể thực hiện theo các bước chi tiết sau đây:
Bước 1: Xác định đoạn thẳng cần vẽ đường trung trực
Giả sử ta có đoạn thẳng AB cần vẽ đường trung trực. Trên giấy, dùng thước thẳng nối hai điểm A và B để tạo thành đoạn thẳng AB rõ ràng, thẳng và chính xác.
Bước 2: Dùng compa để vẽ hai cung tròn cắt nhau
- Đặt mũi compa tại điểm A, mở compa lớn hơn nửa độ dài đoạn thẳng AB, sau đó vẽ một cung tròn cắt phía trên và phía dưới của đoạn thẳng.
- Giữ nguyên độ mở compa, đặt mũi compa tại điểm B, rồi vẽ thêm một cung tròn khác cắt các cung vừa vẽ tại hai điểm, gọi là C và D.
Lưu ý: Nếu bán kính compa quá nhỏ (nhỏ hơn nửa độ dài AB), hai cung sẽ không cắt nhau, vì vậy cần đảm bảo bán kính đủ lớn.
Bước 3: Nối hai giao điểm của hai cung tròn
Dùng thước kẻ nối hai điểm C và D. Đường thẳng CD chính là đường trung trực của đoạn thẳng AB.
Đường này vừa đi qua trung điểm của AB, vừa vuông góc với AB tại trung điểm đó.
Bước 4: Kiểm tra kết quả
- Dùng thước đo góc để kiểm tra góc giữa AB và đường trung trực CD — góc này phải bằng 90°.
- Dùng thước đo độ dài để xác nhận trung điểm M của AB chia đoạn thẳng AB thành hai phần bằng nhau: AM = MB.
Sau khi hoàn thành, ta có đường trung trực của đoạn thẳng AB là đường thẳng đi qua trung điểm M và vuông góc với AB.
Mọi điểm nằm trên đường trung trực đều có khoảng cách bằng nhau đến hai đầu mút A và B.
Tính chất này rất quan trọng trong việc:
- Dựng hình học, xác định tâm của đường tròn ngoại tiếp tam giác.
- Giải bài toán chứng minh hình học như chứng minh hai đoạn thẳng bằng nhau, hai điểm đối xứng nhau qua đường trung trực,…
- Ứng dụng thực tế như trong kỹ thuật, xây dựng hoặc thiết kế — khi cần tìm vị trí cân bằng, chính giữa hoặc điểm cách đều hai vật thể.
-
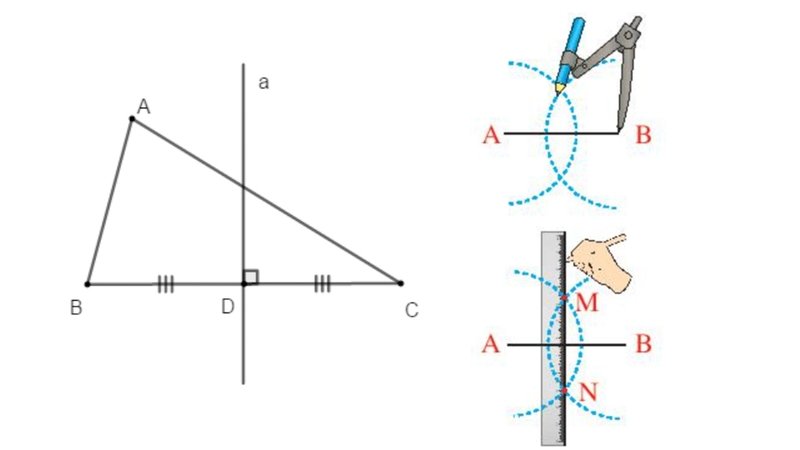
Cách vẽ đường trung trực
Tính chất của đường trung trực là gì?
Đường trung trực của một đoạn thẳng là đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó. Đây là một yếu tố cơ bản trong hình học, có nhiều tính chất quan trọng giúp giải quyết các bài toán dựng hình và chứng minh hình học.
Ngoài định nghĩa cơ bản, đường trung trực còn có nhiều tính chất quan trọng giúp chúng ta giải quyết các bài toán hình học và dựng hình chính xác.
Mọi điểm nằm trên đường trung trực đều cách đều hai đầu mút của đoạn thẳng.
Nếu điểm M nằm trên đường trung trực của đoạn AB thì độ dài MA bằng với MB. Tính chất này giúp ta nhận biết một điểm có thuộc đường trung trực hay không và là cơ sở để xác định vị trí của các điểm trong mặt phẳng hình học.
Ngược lại, mọi điểm cách đều hai đầu mút của đoạn thẳng đều nằm trên đường trung trực.
Nếu một điểm có khoảng cách đến hai đầu mút A và B bằng nhau, thì điểm đó chắc chắn nằm trên đường trung trực của đoạn AB. Hai tính chất này là hai mệnh đề thuận và đảo, thường được sử dụng song song trong các bài toán chứng minh.
Đường trung trực chia đoạn thẳng thành hai phần bằng nhau.
Do đi qua trung điểm của đoạn thẳng, đường trung trực luôn chia đoạn thẳng thành hai phần có độ dài bằng nhau. Đây là đặc điểm giúp phân biệt đường trung trực với các đường khác như phân giác hay trung tuyến.
Đường trung trực vuông góc với đoạn thẳng tại trung điểm.
Đây là một tính chất hình học cơ bản: đường trung trực luôn tạo với đoạn thẳng một góc vuông (90°) tại điểm trung điểm. Tính chất này giúp ta dễ dàng dựng hoặc kiểm tra đường trung trực bằng thước đo góc.
Ba đường trung trực của tam giác luôn cắt nhau tại một điểm.
Trong một tam giác, mỗi cạnh có một đường trung trực riêng. Ba đường trung trực đó luôn đồng quy tại một điểm duy nhất, gọi là tâm đường tròn ngoại tiếp tam giác. Điểm này cách đều ba đỉnh của tam giác và là tâm của đường tròn đi qua cả ba đỉnh.
Từ các tính chất trên, ta thấy rằng đường trung trực là một khái niệm quan trọng trong hình học phẳng. Nó không chỉ giúp xác định vị trí các điểm cách đều hai đầu mút của đoạn thẳng mà còn là công cụ quan trọng trong việc dựng hình, tìm tâm đường tròn ngoại tiếp và giải nhiều bài toán hình học khác.

Đường trung trực của đoạn thẳng AB
Ví dụ minh họa về đường trung trực
Để hiểu rõ hơn về khái niệm đường trung trực, ta hãy cùng xem qua một số ví dụ minh họa cụ thể trong hình học và trong thực tế.
Ví dụ 1: Đường trung trực của đoạn thẳng AB
Giả sử ta có đoạn thẳng AB = 6 cm.
- Trước tiên, ta xác định trung điểm M của đoạn thẳng AB sao cho AM = MB = 3 cm.
- Sau đó, vẽ một đường thẳng vuông góc với AB tại M.
Đường thẳng này chính là đường trung trực của đoạn thẳng AB, vì nó vừa đi qua trung điểm vừa vuông góc với đoạn thẳng.
Mọi điểm nằm trên đường thẳng đó (ví dụ điểm C hoặc D) đều có khoảng cách đến A và B bằng nhau, nghĩa là CA = CB và DA = DB.
Ví dụ 2: Ba đường trung trực trong tam giác
Xét tam giác ABC bất kỳ.
- Ta vẽ đường trung trực của cạnh AB, của cạnh AC và của cạnh BC.
- Ba đường trung trực này luôn cắt nhau tại một điểm duy nhất, gọi là tâm đường tròn ngoại tiếp tam giác (O).
Điểm O có đặc điểm là cách đều ba đỉnh A, B và C, nghĩa là:
OA=OB=OC
Nhờ tính chất này, ta có thể dựng một đường tròn đi qua cả ba đỉnh của tam giác – đó chính là đường tròn ngoại tiếp.
Ví dụ 3: Ứng dụng trong thực tế
Giả sử bạn muốn đặt một cột đèn sao cho cách đều hai ngôi nhà A và B.
Để xác định vị trí thích hợp, ta chỉ cần xác định đường trung trực của đoạn thẳng nối A và B.
Mọi điểm trên đường trung trực đó đều cách đều hai ngôi nhà, nên nếu đặt cột đèn ở bất kỳ vị trí nào trên đường này, ánh sáng sẽ được phân bố cân đối và công bằng đến cả hai bên.
Qua những kiến thức trên, chúng ta có thể hiểu rõ đường trung trực là gì, cũng như nắm được các tính chất, cách vẽ và ứng dụng của nó trong học tập và đời sống. Đường trung trực không chỉ là một khái niệm cơ bản trong hình học mà còn là nền tảng để giải nhiều bài toán liên quan đến đối xứng, khoảng cách và đường tròn ngoại tiếp tam giác. Việc hiểu và vận dụng đúng đường trung trực sẽ giúp bạn học tốt hơn môn Toán và ứng dụng hiệu quả vào thực tế.
>> Tham khảo: Trồng răng giả tháo lắp


